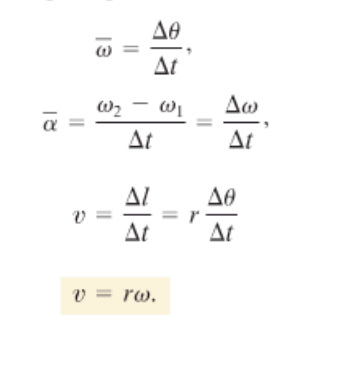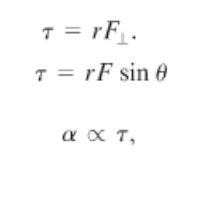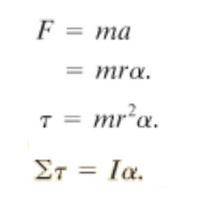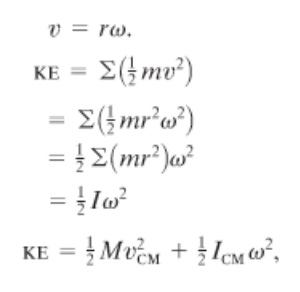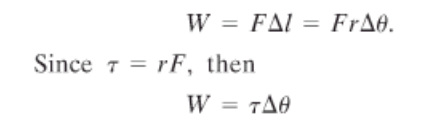Rotational Motion
Note: according to the topic outline on College Board, only torque and rotational statics will be on the Physics B exam. So, the first section will focus on the basics of rotational motion and the topics covered in the exam, and the second part will be everything else.
Part 1
Basics
|
1. We will be dealing with rigid objects (every point on the object is fixed relative to each other).
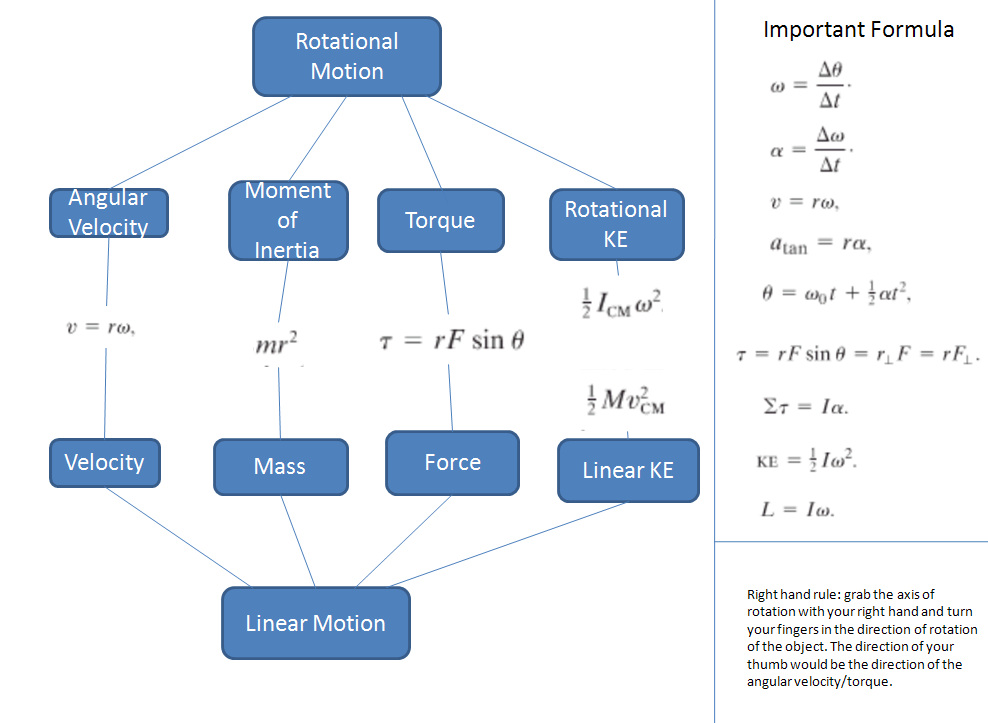
2. In rotational motion, we deal with angular velocity, which is the angular displacement over time. An important point to notice is that every point on a rotating, rigid object has the same angular velocity, and to find the linear velocity, simply multiply the radius to the angular velocity. 3. Just like linear acceleration, angular acceleration is the change in angular velocity over time. Note: θ is usually measured in radians. |
Torque
|
Torque is the perpendicular force times the lever arm.
Torque is also called moment of force because it’s analogous to force in linear kinematics. Lever Arm is the perpendicular distance from the axis of rotation to where the force acts. When we consider torque, we use the perpendicular force because no torque is created by the parallel force. That is why we need to multiply sineθto the force. Note that although torque and energy have the same units, they are very different. Torque is a vector while energy is a scalar. |
Part 2 (Physics C stuff)
Moment of Inertia
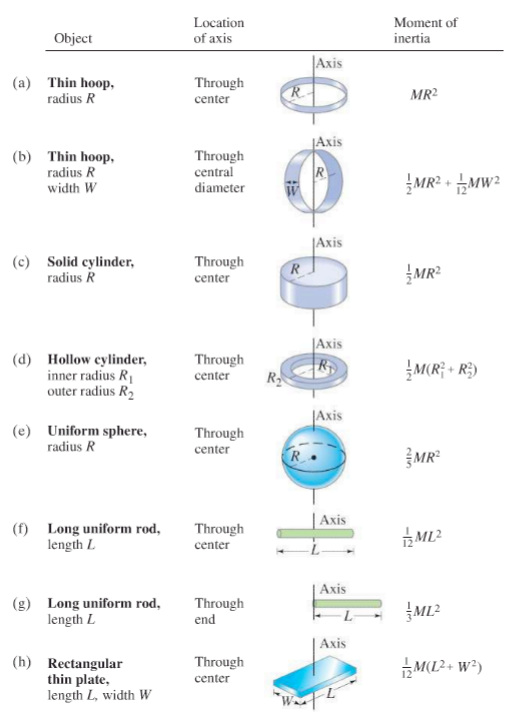
List of moments of inertia
|
We can get the kinetic energy of the rotating object using the same formula as linear motion, just by substituting several factors in.
First of all, velocity, in rotational motion, is equal to ωr, and we will substitute that into our KE function. We do algebra and we get KE is the moment of inertia (that’s why it’s similar to mass) times angular velocity squared. The KE of a rolling object has both linear KE and rotational KE, so it is simply the sum of both KEs. |
Just like linear momentum, angular momentum, L, is also conserved if the net torque on the object is 0. This is important because changes in the moment of inertia will correspond to a change in the angular velocity. There is a video in the extra section that illustrates the conservation of linear momentum.
Right hand rule: grab the axis of rotation with your right hand and turn your fingers in the direction of rotation of the object. The direction of your thumb would be the direction of the angular velocity/torque.
Right hand rule: grab the axis of rotation with your right hand and turn your fingers in the direction of rotation of the object. The direction of your thumb would be the direction of the angular velocity/torque.