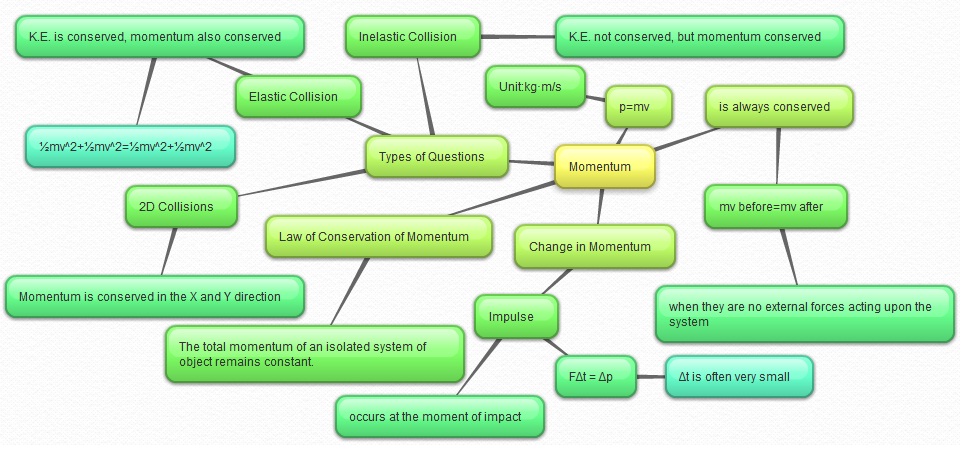
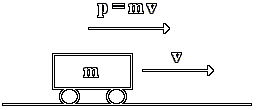Momentum
Equations:
There are two, and only two, equations that you get to play with:
1) This is the equation for momentum.
p=mv
There are two, and only two, equations that you get to play with:
1) This is the equation for momentum.
p=mv
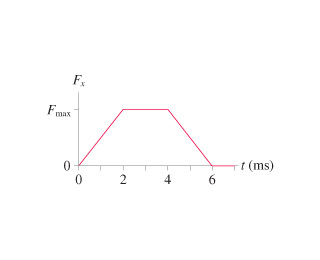
2) This is the equation for impulse.
Impulse = FΔt = Δp
Impulse = FΔt = Δp
Derivation: How did we get Impulse from Momentum?
Well, we understand that,
p=mv
Since Impulse is defined as the change in momentum,
Δp=mΔv
=m(aΔt)
=maΔt
=(ma)Δt
= FΔt
From this equation, we can also see that impulse is the amount of force acting upon an object in a given period of time.
Well, we understand that,
p=mv
Since Impulse is defined as the change in momentum,
Δp=mΔv
=m(aΔt)
=maΔt
=(ma)Δt
= FΔt
From this equation, we can also see that impulse is the amount of force acting upon an object in a given period of time.
Types of Questions You Will Encounter and How to Approach Them!
A.Systems of Particles, Linear Momentum
1. Impulse and Momentum: You should understand impulse and linear momentum so you can:
a.Relate mass, velocity, and linear momentum for a moving body, and calculate the total linear momentum of a system of bodies.
By using the momentum equation.
b.Relate impulse to the change in linear momentum and the average force acting on a body.
Just use the impulse equation. If you have a collision, time, and a force in a problem, think’ impulse’.
2.Conservation of Linear Momentum, Collisions
a.You should understand linear momentum conservation so you can:
(1) Identify situations in which linear momentum, or a component of the linear momentum, is conserved.
The momentum of an isolated system (no outside forces) is conserved in any interaction.
(2)Apply linear momentum conservation to determine the final velocity when two bodies that are moving along the same line, or at right angles, collide and stick together, and calculate how much kinetic energy is lost in such a situation.
After the collision both bodies have the same velocity.Therefore: m1v1+m2v2=(m1+m2)vf
(3)Analyze collisions of particles in one or two dimensions to determine unknown masses or velocities, and calculate how much kinetic energy is
lost in a collision.
3. Collisions
a. Elastic: K.E. is conserved.
½mAvA^2+½mBvB^2=½mAv'A^2+½mBv'B^2
b. Inelastic: K.E. is not conserved.
2D Collisions: If the two bodies are moving at right angles, then the vertical momentum is conserved and the horizontal momentum is conserved, so you can write equations for the conservation of momentum in the x and y directions.
A.Systems of Particles, Linear Momentum
1. Impulse and Momentum: You should understand impulse and linear momentum so you can:
a.Relate mass, velocity, and linear momentum for a moving body, and calculate the total linear momentum of a system of bodies.
By using the momentum equation.
b.Relate impulse to the change in linear momentum and the average force acting on a body.
Just use the impulse equation. If you have a collision, time, and a force in a problem, think’ impulse’.
2.Conservation of Linear Momentum, Collisions
a.You should understand linear momentum conservation so you can:
(1) Identify situations in which linear momentum, or a component of the linear momentum, is conserved.
The momentum of an isolated system (no outside forces) is conserved in any interaction.
(2)Apply linear momentum conservation to determine the final velocity when two bodies that are moving along the same line, or at right angles, collide and stick together, and calculate how much kinetic energy is lost in such a situation.
After the collision both bodies have the same velocity.Therefore: m1v1+m2v2=(m1+m2)vf
(3)Analyze collisions of particles in one or two dimensions to determine unknown masses or velocities, and calculate how much kinetic energy is
lost in a collision.
3. Collisions
a. Elastic: K.E. is conserved.
½mAvA^2+½mBvB^2=½mAv'A^2+½mBv'B^2
b. Inelastic: K.E. is not conserved.
2D Collisions: If the two bodies are moving at right angles, then the vertical momentum is conserved and the horizontal momentum is conserved, so you can write equations for the conservation of momentum in the x and y directions.
Joycelyn Su