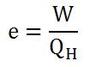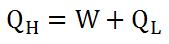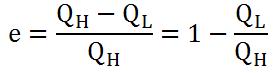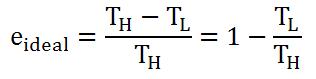Heat Engines
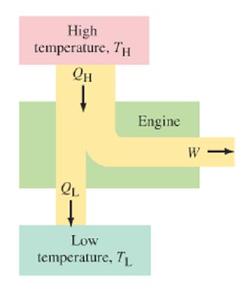
A heat engine is any device that changes thermal energy into mechanical work. This usually happens when heat is allowed to flow from a high temperature to a low temperature, as indicated in the diagram to the left.
To determine how "good" a heat engine is, it is necessary to calculate its efficiency. To calculate efficiency, we divide the amount of work it does by the heat input at the high temperature (equation 1). According to equation 2, work equals the heat input of the high temperature minus the heat input of the low temperature. This makes sense, since part of the heat input is used to do work, while the remainder cools down, making the low temperature input (see the diagram).
After substituting everything in and simplifying, we get the final equation for efficiency (equation 3).
To determine how "good" a heat engine is, it is necessary to calculate its efficiency. To calculate efficiency, we divide the amount of work it does by the heat input at the high temperature (equation 1). According to equation 2, work equals the heat input of the high temperature minus the heat input of the low temperature. This makes sense, since part of the heat input is used to do work, while the remainder cools down, making the low temperature input (see the diagram).
After substituting everything in and simplifying, we get the final equation for efficiency (equation 3).
Carnot Engines
Carnot engines, or "ideal engines," contains of four thermodynamic processes. Two of them are adiabatic, where Q=0, and two of them are isothermal, where there's no change in temperature. Because this is the ideal engine, each process could also be done reversibly. In all real engines, however, it is irreversible. The diagrams and flash files below further explains how a Carnot engine works.
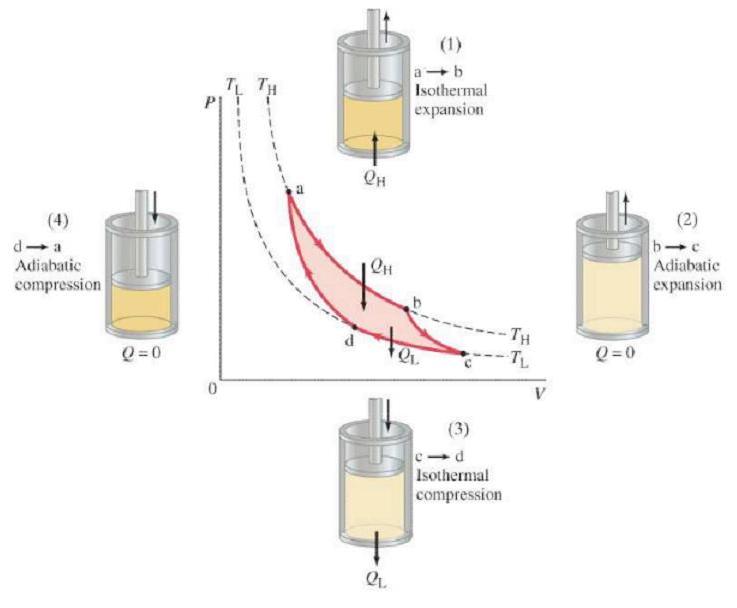
CARNOT ENGINE: 1. Gas expanded isothermally, with the addition of Q(H), along the path ab at temperature T(H).
2. Gas expands adiabatically from b to c; no heat exchanged, but T(H) becomes T(L).
3. Gas compressed at constant temperature T(L), path cd; heat Q(L) flows out.
4. Gas compressed adiabatically, path da, back to original state (1).
In Carnot's ideal reversible engine, Q is proportional to T. Thus, efficiency of an ideal engine could also be written as:
Thus, 100% efficiency can never happen; T(L) has to be at absolute zero (0 K).