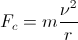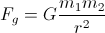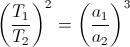Chapter 5: Circular Motion, Gravitation
This is pretty self-explanatory. This chapter focuses on centripetal and gravitational forces.
First of all, let's begin with an explanation of circular motion.
First of all, let's begin with an explanation of circular motion.
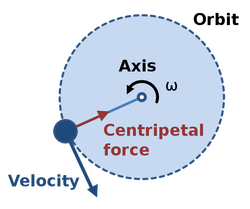
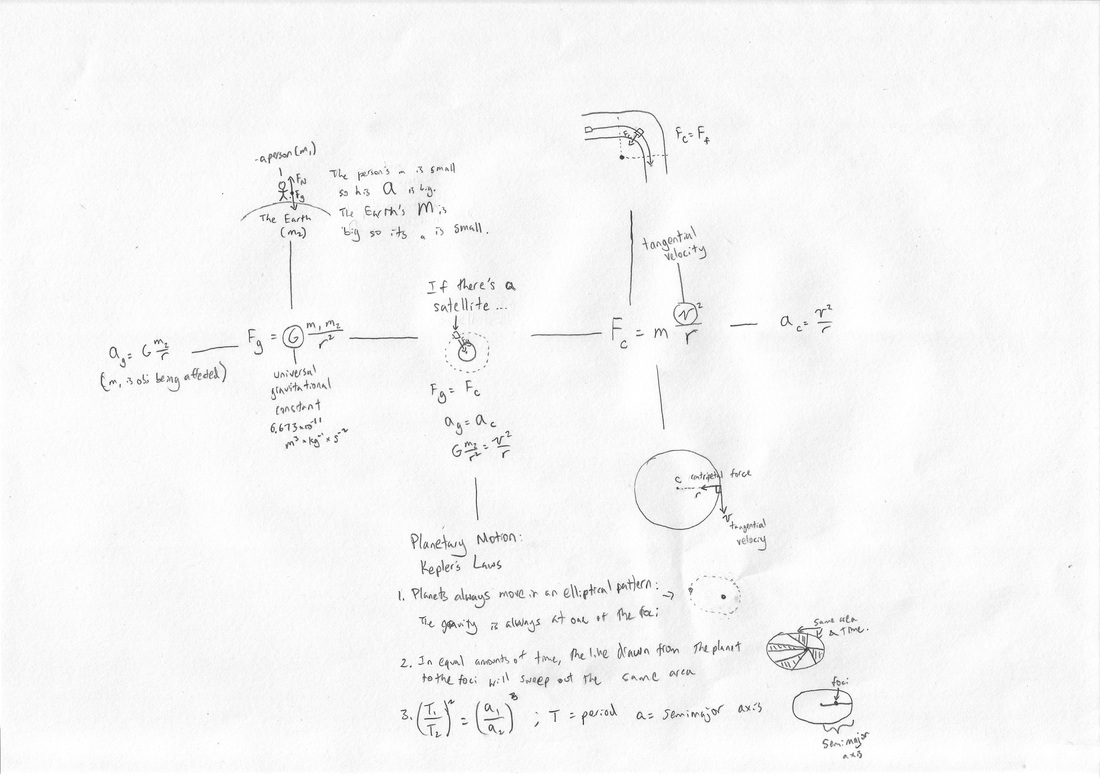
As we can see, there is a velocity vector that is tangent to the force vector. The force itself is pulling towards the center of the circle, while the velocity wants to go tangentially. The "centrifugal force" that most people talk about does not exist. Rather, "centrifugal force" is the momentum of the object (tangential velocity) vs. the centripetal force (which is the acceleration of the object).
Centripetal Force Equation
XKCD is awesome
As you can see, Mr. Bond is correct. Black Hat failed AP Physics B.
(there's a cool video in the demo section)
Gravitation:
The essential thing to note is the gravitational equation, which is down below (all equations are down there by the way). Basically, what it says is that no matter what mass the two objects have, and no matter how far away they are, there is still gravity between them.
However, seeing as G, the gravitational constant, is 6.67300 × 10^-11, the masses would have to be extremely large for the gravitational force to have a tangible effect.
If satellites are viewed in terms of uniform circular motion, the two can easily be used to determine the mass of a large object or determining the force necessary to keep it from falling to the source of gravitation.
(there's a cool video in the demo section)
Gravitation:
The essential thing to note is the gravitational equation, which is down below (all equations are down there by the way). Basically, what it says is that no matter what mass the two objects have, and no matter how far away they are, there is still gravity between them.
However, seeing as G, the gravitational constant, is 6.67300 × 10^-11, the masses would have to be extremely large for the gravitational force to have a tangible effect.
If satellites are viewed in terms of uniform circular motion, the two can easily be used to determine the mass of a large object or determining the force necessary to keep it from falling to the source of gravitation.
Gravitational Force Equation
Kepler's laws of planetary motion concerns how planets move in space.
The first law states that planets move in an elliptical, not circular motion.
The second law states that a line connected from a planet to the star will sweep out equal areas in a certain time period (another cool demo is in the demo section).
The third law states essentially the equation below: (T is period, a is the semimajor axis)
The first law states that planets move in an elliptical, not circular motion.
The second law states that a line connected from a planet to the star will sweep out equal areas in a certain time period (another cool demo is in the demo section).
The third law states essentially the equation below: (T is period, a is the semimajor axis)
Kepler's Third Law
